判断数值天气预报准确率是否显著地高于盲目预报准确率(仅以降雨预报为例,且不分雨量大小),那就要用到数理统计学中的差异显著性检验。其计算公式为:
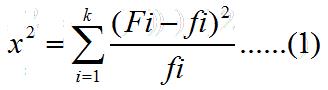
式(1)中,Fi是预报正确与错误的实际次数,fi为盲目预报的正确与错误的理论次数;k为项数,对不分大小的降雨预报来说,k=2,即只分预报正确和错误两种情况。式中求出的x2就是差异显著性检验值(俗称“卡平方值”)。
例如,在某地82天的数值天气预报中,24-36小时(即明天白天)的预报,共报25次有雨,报对19次,报错6次,报雨报对准确率为76.0%(19/25)。在这82天中,实际有降雨的天数为24天,盲目预报降雨的理论准确率为24/82=29.2%,盲目预报报对的理论次数为25*24/82=7.3171次。盲目预报报错的理论次数为25*(82-24)/82=17.6829次。
这样,卡平方值求算如下:
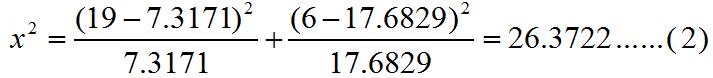
x2值26.3722大于自由度为1,信度为0.01时的标准x2值6.64。因此证明了,预报准确率极显著地高于盲目预报准确率,对该地24-36小时(即明天白天)的降雨预报是有效的。
如果x2值小于自由度为1,信度为0.05时的标准x2值3.84,则预报准确率与盲目预报准确率差异不显著,这时可断定该时段降雨预报是无效的。
如果x2值,介于6.64和3.84之间,则差异有些显著,该预报可参考。
上面的计算过程是不挺简单呢?用此方法,每个预报员都可以计算一下,别人给你提供的数值天气预报,各个预报时段的预报结果是否是有效的。
判断数值预报时效,除了差异显著性检验方法以外,还有相关系数法,这里就不再一一介绍了。
下一节将发布数值天气预报时效2019-2022年连续四年的统计检验结果简报。